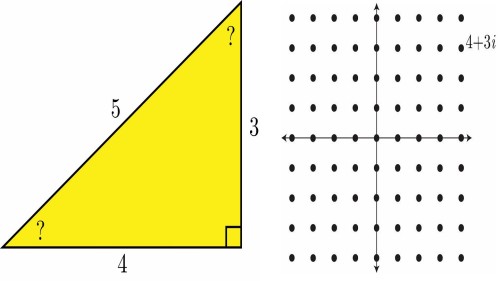
What are the acute angles in a 3-4-5 triangle? Are they nice, say rational in degrees? We'll use the Gaussian integers—the square lattice in the complex numbers—to study those questions. Like the ordinary integers, the Gaussian integers possess unique factorization. The existence of the greatest common divisor is the crucial step in proving that fact. We present a simple geometric argument for that step using repeated subtraction. With unique factorization in hand, we characterize the Gaussian integers having a positive integer power that is real. That characterization sheds light on the nature of the acute angles in Pythagorean triple triangles.
Join us on Monday, Feb. 24, at 3:10 p.m. in Hayes 109 to hear this exciting presentation from Dr. Jack Calcut, Professor of Mathematics at Oberlin College and Conservatory. We hope to see you there!