Haroun Meghaichi of The Ohio State University will be visiting campus to discuss his research using differential geometry and numerical analysis in solving interface problems.
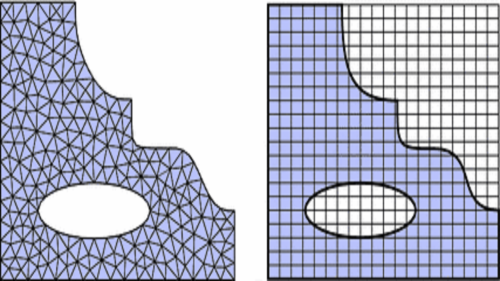
"Interface problems naturally arise when modeling physical phenomena occurring across multiple physical media. Mathematically, they are described by differential equations with discontinuous coefficients that model material properties. These discontinuities pose challenges to classical numerical methods (e.g., finite difference and finite element methods), which we address by developing a high-order finite element space that leverages the local geometry of the interface.
"In this talk, I will start from the basics of the finite element methods for elliptic problems and the challenges therein, then I will cover the recent developments on unfitted finite element methods for interface problems with a focus on the geometry-conforming immersed finite element method."
Join us on Monday, April 7, at 3:10 p.m. in Hayes 109 to hear this exciting presentation from Haroun Meghaichi, assistant professor of mathematics at The Ohio State University. We hope to see you there!